正三角形の1辺の長さをaとするすると PB・a+PC・a=AP・a 次のように証明しても良い. BPCをBの周りに60°回転した三角形を BP'Aとする(上図). このとき, この命題は逆もなりたつ.すなわち不等辺三角形 不等辺三角形 不等辺三角形の選択した3つの入力値から他の要素の値を計算します。 このページの先頭へ概要 三角形の三辺が x, y, z で最大辺が z とすれば、三角不等式は が成り立つことを主張している 。 等号が成立するのは三角形が面積 0 に退化したときに限る。 ユークリッド幾何学ほかいくつかの幾何学において、三角不等式は距離に関する定理であって、ベクトルやベクトルの長さ
プンチ ラマイ Montessori 三角形のお仕事
不等辺三角形 辺の長さ 比
不等辺三角形 辺の長さ 比-三角形の存在条件三角形の存在条件とは三角形の存在条件とは, 3つの数 が与えられたときに, 3辺の長さがそれぞれ であるような三角形が存在するための条件です 定理 3辺の長さがそれぞれ である三角形が存在するための必要十分条件は,が成り立つことである2 高さ (h) =SQRT (3)/2*B1 3 3辺の長さ (L) =3*B1 4 面積 (S) =SQRT (3)/4*B1^2




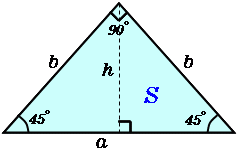
二等辺三角形の面積を求める算数の公式は
正弦定理から,三角形の辺の長さを求める計算について ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわかりま(1) 右図のように三辺の長さだけが与えられた三角形で、「高さAH」や「三角形の面積」を求めるには BH=xとおいて(このときCH=6xとなります) AHの長さ(の2乗)を2とおりの方法で表わせば解けます。 (√13) 2x 2 = AH 2 = 5 2(6x) 2 (√13) 2x 2 = 5 2(6x) 2 13x 2 =25(3612xx 2) 24=12x x=2余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます: a 2 =b 2 c 2 −2bc cos A この式をよく見ると、 「右辺は辺の長さだけ」 でできており、 左辺は角度だけ でできています。 したがって、この式を利用すると 「3辺の長さ」から、 「角 A 」 を求める ことができます。 (正確には、角 A そのものではなく cos A が求まりますが
三角形の3辺が与えられたときの面積の求め方 「3辺の長さが,5,4,7の三角形の面積を求めよ。」という問題がわかりません。面積を求めるときは,公式 S=1/2bc sinA に当てはめればいいことは1 三角不等式を理解します。 この定理は、三角形の二辺の和は残りの一辺よりも大きくなるということを述べています。 これが三つの組み合わせ全てで成り立つ場合、三角形ができます。 三つの組み合わせを一つ一つ確認して、三角形が成立するか調べる必要があります。 三角形の辺の長さをa、b、cとすると、定理は次のように表せます。 ab > c、 ac > b、 bc > a三角形の 3 つ辺のうち一つを選んで底辺とし、その対頂点から底辺(またはその延長)に下した垂線から、三角形が切り取る線分(線分の長さ)を、三角形の高さという。どの辺を底辺と見るかによって、三角形には 3 つの高さを考えることができる。
1) 単元名 第4学年「三角形と角」 (2) 教材観 第4学年における「三角形」の学習は,辺の長さに着目して三角形を分類しながら,二等辺三角形や正三角形などの図形を理解させる。 おはようございます。 三角不等式、ab≦ab は、三角形の辺の長さの間の関係から示されるそうですが、三角形の辺の長さ(の間の関係)と、ab≦ab が、どうつながるのかが分かりません。ちなみに、a,b は辺の長さですよね二等辺三角形(にとうへんさんかくけい、英 isosceles triangle )は、三角形の一種で、3 本の辺のうち(少なくとも)2 本の辺の長さが等しい図形である。 長さの等しい 2 辺を等辺といい、残りの 1 辺を底辺とよぶ。2 本の等辺が共有する頂点をとくに二等辺三角形の頂点という。



計算




二等辺三角形の面積を求める算数の公式は
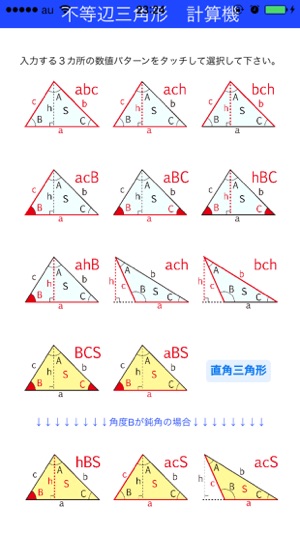
2 回答 このように、不等辺三角形の2つの辺の長さと このように、不等辺三角形の2つの辺の長さと その間の角の角度がわかっている時に、 残ったもう一つの辺の長さを求める公式がわからないのですが、どのような公式を使えば良いのでしょうか? できれば、公式の名前と内容を一緒に教えてもらえるとありがたいです! 数学 ・ 6,642 閲覧 ・ xmlns="http//wwww3org5年 算数 学研教育情報資料センター 学習相談 小/算数/5年/数量関係/ 文字と式/理解シート 三角形の面積から,辺のすなわち、三角形を構成する3辺の長さを a,b,c とするとき、次の三つの不等式が成り立つ。 a < bc;



Triangle Select Im App Store




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
辺の長さが2桁でも気にすんな。 三平方の定理(ピタゴラスの定理)の公式にぶち込めばいいんだ。 x² = 5² 12² x = 13 直角三角形と言えども、いつも右下に直角が来るとは限らんぞ。 わたしの場合、決まった三辺の長さで三角形を書くとすれば まず一辺目の長さのLINEを書き、 その線の両端を中心とした他の二辺と同じ半径の円を描いて 2つの円の交点と線の端点をスナップさせてLINEと引く みたいに描きます。 外していたらごめん 24 不等辺三角形 3辺の値が全て異なる場合、画面に「不等辺三角形」と出力する。 25 異常処理 三角形の判定をする場合は、以下を考慮すること
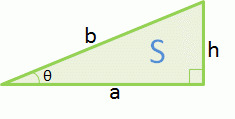



三角形の公式 Wakatta
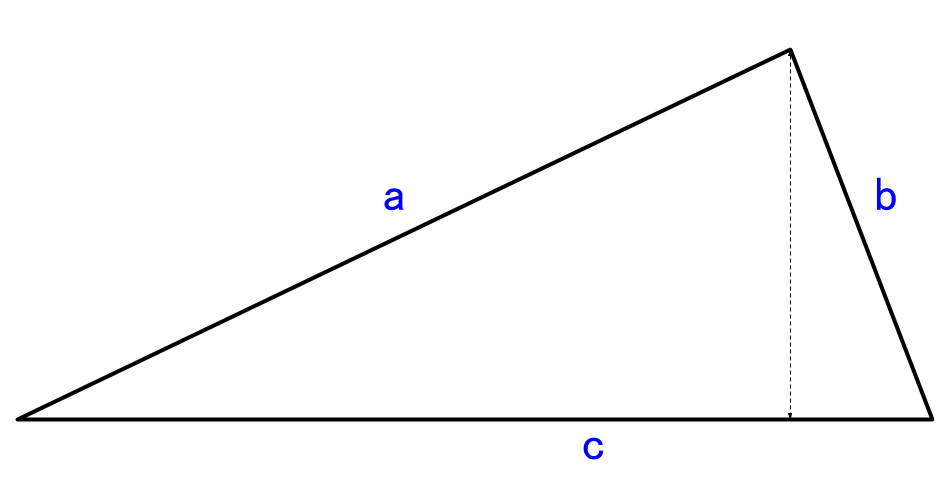



ヘロンの公式 計算機 三角形の面積と高さを 3辺の長さから計算します やまでら くみこ のレシピ
<不等辺三角形> 3辺(ヘロンの公式)、2辺と高さ、2辺と夾角、辺と高さと角、2角と夾辺、2角と高さ、それぞれから各種計算 計算結果:辺、高さ、各角度、面積、周囲の長さ <四角形・多角形>フジテレビ金曜プレステージ 浅見光彦シリーズ49「不等辺三角形」 《放送日》 平成26年1月17日(金) 《原作》 内田康夫「不等辺三角形」徳間文庫刊 《脚本》 峯尾基三 《監督》 柿沼竹生 《出演》 中村俊介、榎木孝明、野際陽子三角形の半周長を見つけるための方程式は次のとおりです。 S = a b c / 2。まず、三角形の3辺すべてを合計します。これは、a b cを意味します。 3つの数値をすべて合計したら、合計を2で割ります。例を見てみましょう。 a b cを合計します:3 4 5 = 12。 12を2で割ります:12/2 = 6。したがって、三角形の半周長(S)は6です。
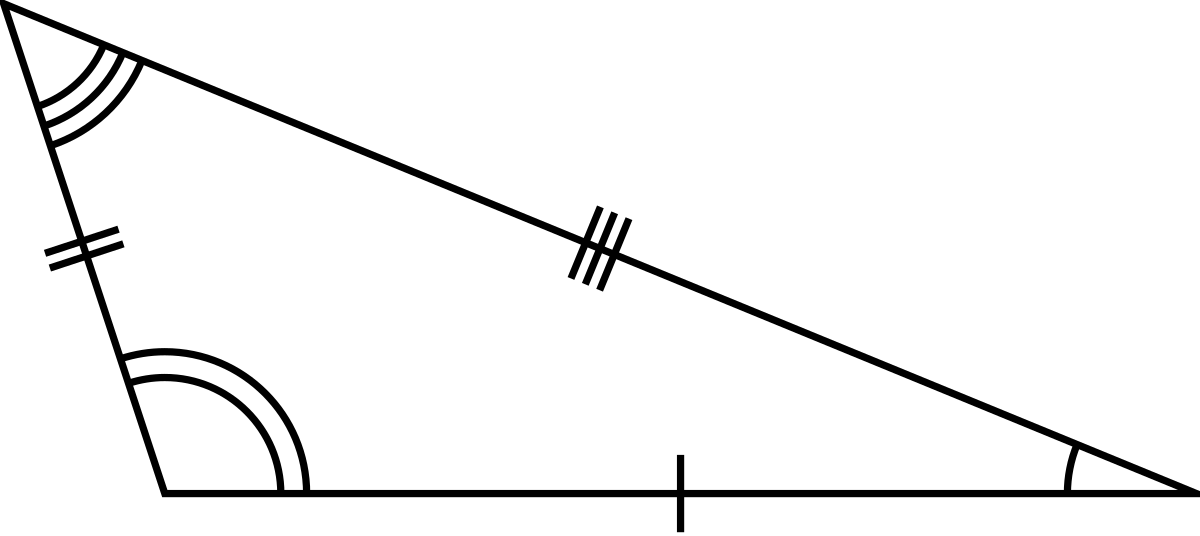



不等辺三角形 ウィクショナリー日本語版




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ
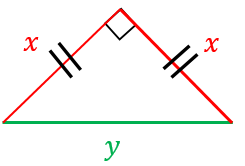
「三角形が成立する→三角不等式が成立する」を証明します。 寄り道した方が距離が長くなる という直感に従うと自明ですが,一応きちんと証明しておきます。 証明 三辺の長さが a,他の辺の長さを $x$、斜辺の長さを $y$ とすると、三平方の定理より、 $x^2x^2=y^2$ です。 つまり、$2x^2=y^2$ です。 この両辺のルートを取ると、$\sqrt{2}x=y$ となります。 つまり、斜辺の長さは他の辺の長さの $\sqrt{2}$ 倍です!ふとうへん‐さんかくけい不等辺三角形 どの辺の長さも等しくない三角形。 出典 小学館 デジタル大辞泉について 情報 凡例




二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4




小学6年生で三角形の面積求め方わかりません 小学6年生の親です 学 数学 教えて Goo
Amazonで内田 康夫の不等辺三角形 (講談社文庫)。アマゾンならポイント還元本が多数。内田 康夫作品ほか、お急ぎ便対象商品は当日お届けも可能。また不等辺三角形 (講談社文庫)もアマゾン配送商品なら通常配送無料。不等辺三角形の選択した3つの入力値から他の要素の値を計算します。 入力指定 3辺abc 2辺abと高さ (Cは鋭角) 2辺abと高さ (Cは鈍角) 2辺bcと高さ (BとCが鋭角) 2辺bcと高さ (BかCが鈍角) 2辺abと夾角C 辺aと高さと角C 2角BCと夾辺a 2角BCと高さ 面積と2辺ab (Cは鋭角) 面積と2辺ab (Cは鈍角) 面積と2角BC 面積と辺aと角C 面積と高さと角C4 9 = c × c 13 = c × c よって、長い辺の長さは c = 13 (二乗して 13 になる正の数)となります。 では、 13 はどれくらいの長さでしょうか? 3 × 3 = 9 c × c = 13 4 × 4 = 16 なので、 13 は 3 より大きくて 4 より小さい数だと分かります。 もう少しきちんと計算すると、




直角二等辺三角形 Wikiwand



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋
三角形を成り立たせる3辺 (三角形の成立条件) 三角形のどの辺の長さも他の二辺の長さの和より小さい。すなわち、三角形を構成する3辺の長さを a,b,c とするとき、次の三つの不等式が成り立つ。 a < bc;向かい合った辺の長さが同じです。 C 向かい合った角の大きさが同じです。 平行四辺形について知っていることを発表させることにより,図形の構成要素である角や辺,平行などの観点に目を向けさせる。 2 ③(不等辺三角形)と同じ仲間の図形を考える。 T 三角不等式は 数学的帰納法 により、任意の折線に関する命題に拡張することができる。 すなわち、そのような折線の全ての辺の長さの和は、その折線の二端点を直線で結んだ長さよりも小さくなることはない。 特にその帰結として、多角形のどんな長さ




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく
不等辺三角形・・・の面積の表し方を大至急教えて下さいヘロンの公式を使用すれば、3辺の長さから三角形の面積が求められます。3辺の長さを a,b,c とすれば、s=(abc)/2 としてS=√{s(sa)(sb)(sc)} となります。




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
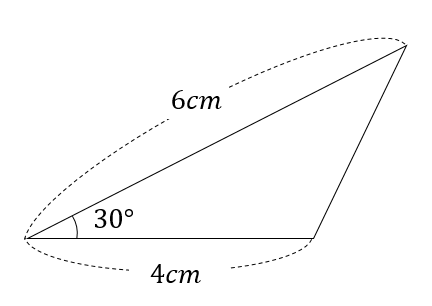



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ




辺の長さが全て整数となる直角三角形と二等辺三角形で周の長さも面積も共に等しい組 あなたも社楽人
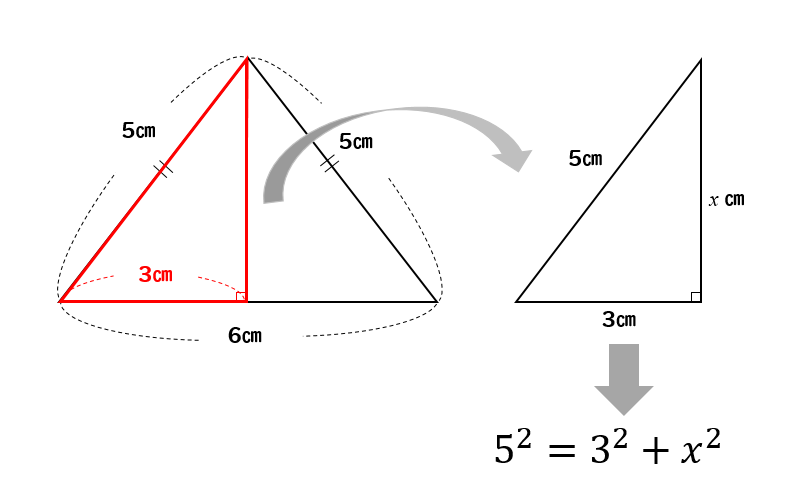



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
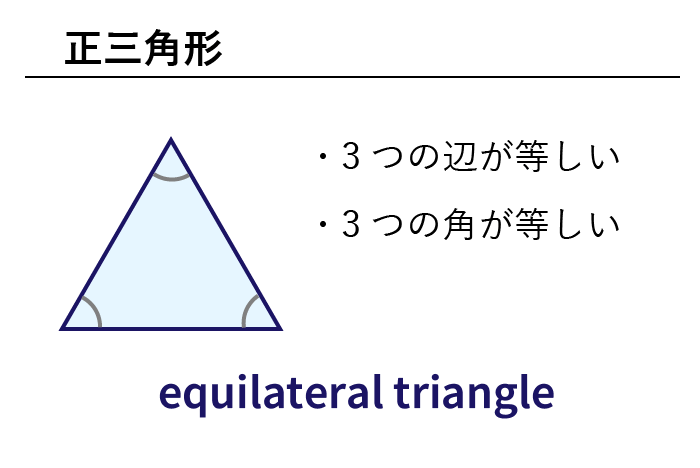



数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
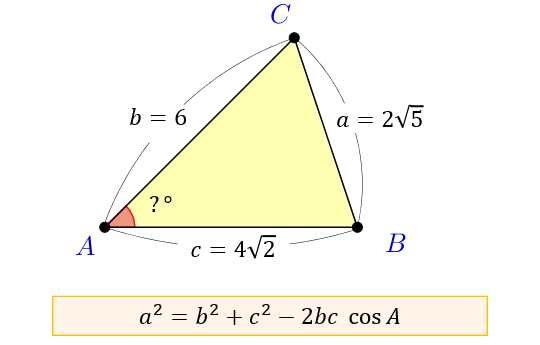



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強
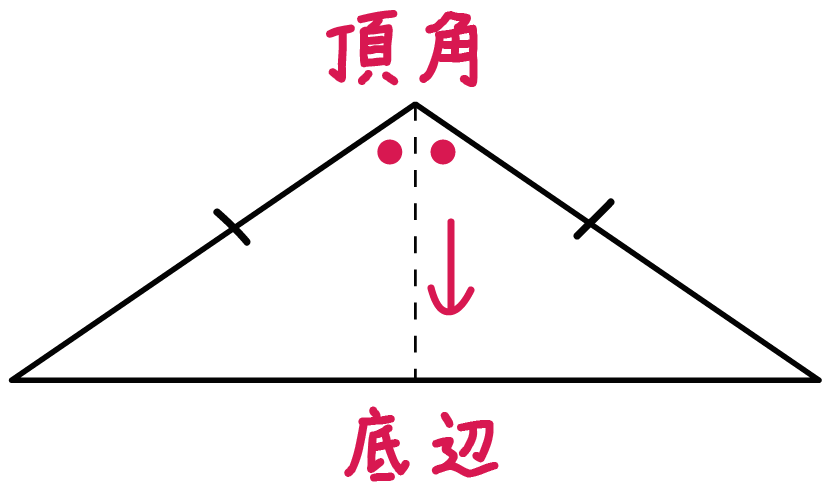



二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1
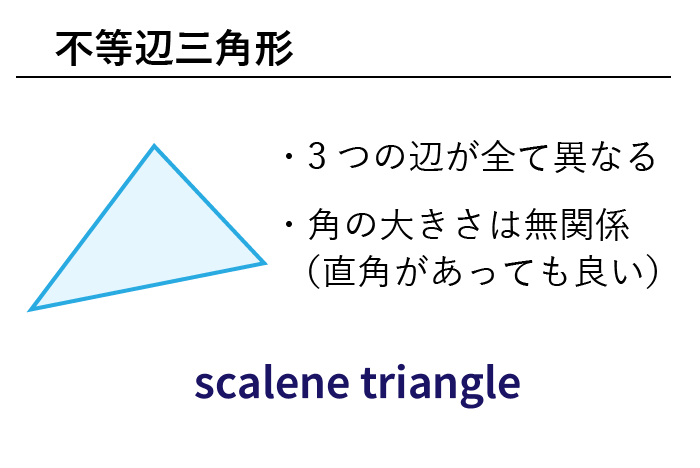



数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋
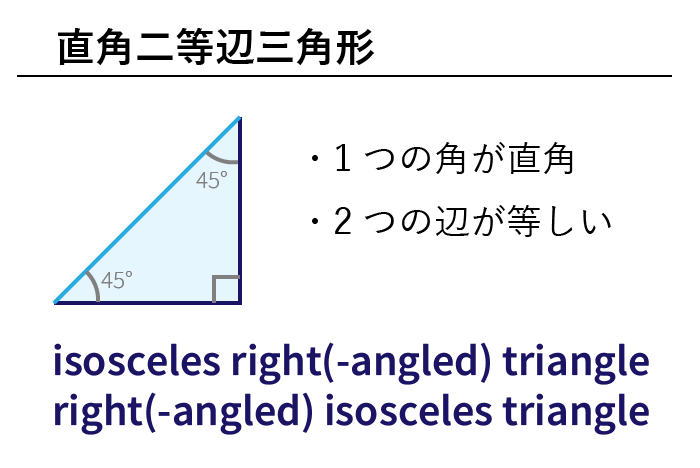



数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo
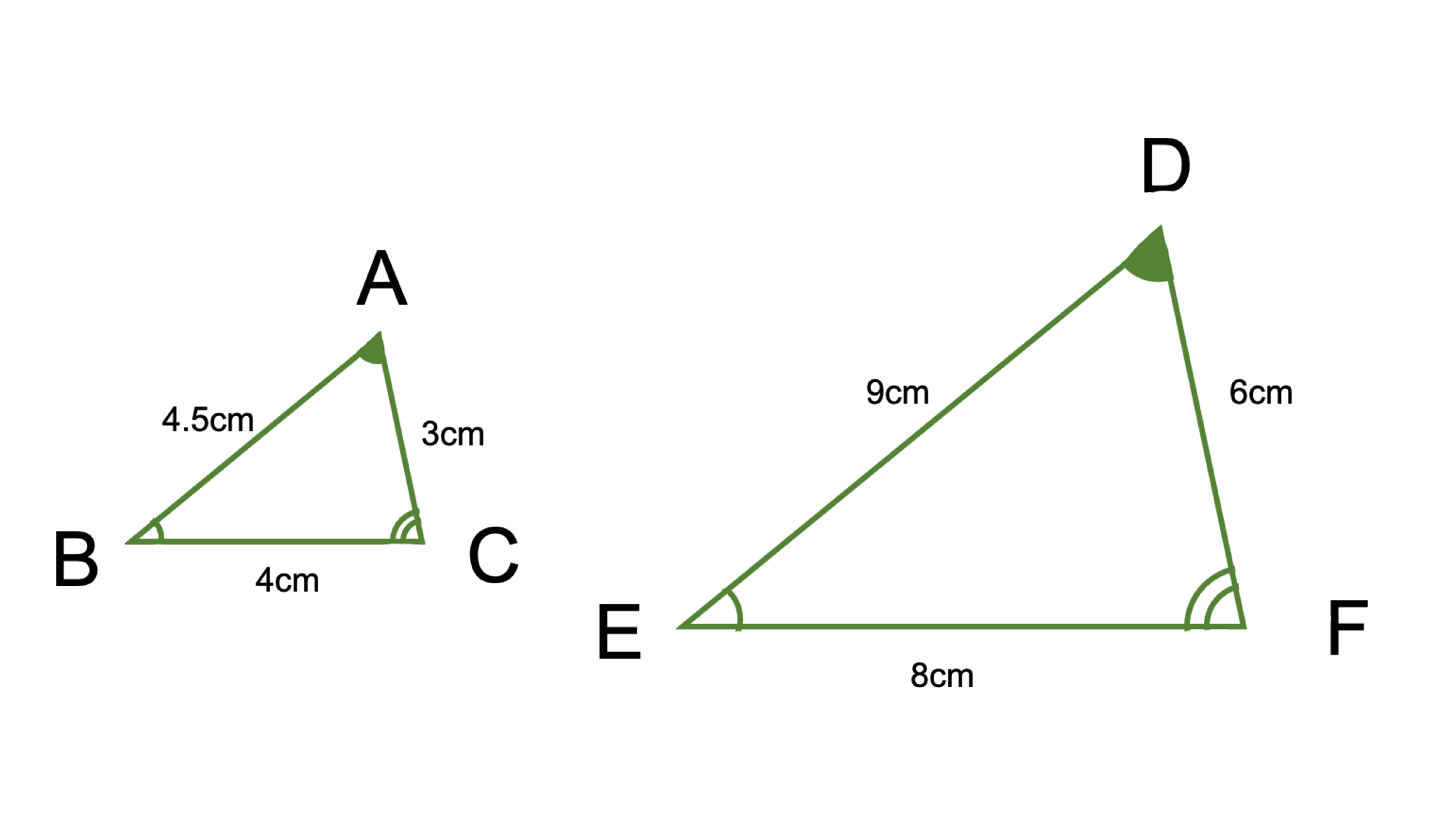



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




二等辺三角形 Wikipedia




メルカリ 幾何学模様と不等辺三角形のデザイン 幅91cm 長さ0cm 生地 糸 1 380 中古や未使用のフリマ




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




愛の不等辺三角形 漱石から読み解く 本人描いた図も 朝日新聞デジタル



不等辺三角形の高さについてです 画像のa B C 角a Yahoo 知恵袋



3
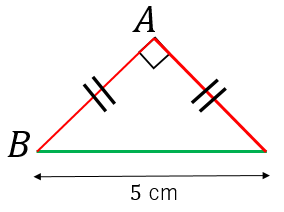



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
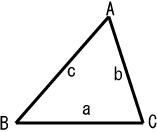



三角形 Wikipedia



Math 90 30 60 の直角三角形 辺の長さで成り立つこと 働きアリ



不等辺三角形のフラクタル 宇田川辰彦監修 庭師が教える 図解 日本庭園の見方 楽しみ方 勉強メモ Togetter



幼児教室は ピグマリオン大阪本部 江坂教室 吹田市 英才児養成専門の幼児教室
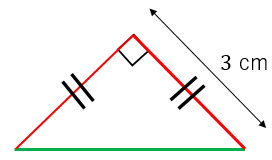



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
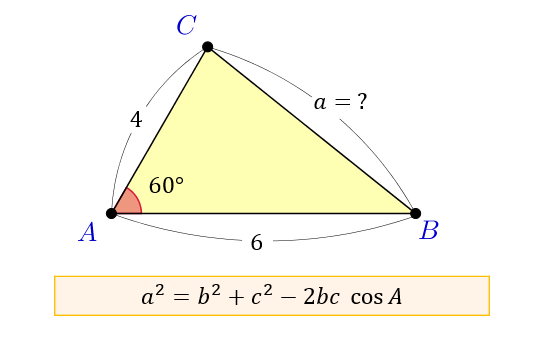



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




二等辺三角形や直角三角形って英語で何て言うの 三角形の種類について 40代 50代 60代 シニア 初心者からやり直し英会話 英語学習法




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
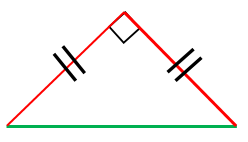



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



プンチ ラマイ Montessori 三角形のお仕事




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



11 7 数学 図形 これは 不等辺三角形 ふとうへんさんかっけい ですか 辺が揃ってない三角形の話 のっぽさんの勉強メモ




建築積算の数量算出中によく使う計算 直角三角形の斜辺の長さ



3




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強



ゆっるゆる アクアリウムと日本の庭園にみる伝統石組みレイアウト Mobi Aqua



不等辺三角形角度について教えて下さい 辺aが1367辺bが473 Yahoo 知恵袋




13 マイヤーズの三角形 その テスターちゃん 4コマ漫画



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比



三角形の英語 正三角形 二等辺三角形 直角三角形など 英語独学マスター




3 おかしな不等辺三角形 Imujii S Page




直角二等辺三角形 Wikipedia




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



ヘロンの公式 不等辺三角形などの面積 角度 高さ 数学 エクセルマニア



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




三角形の英語 正三角形 二等辺三角形 直角三角形など 英語独学マスター



三角形 辺 の 長 さ 比率 238n424 Proxydns Com
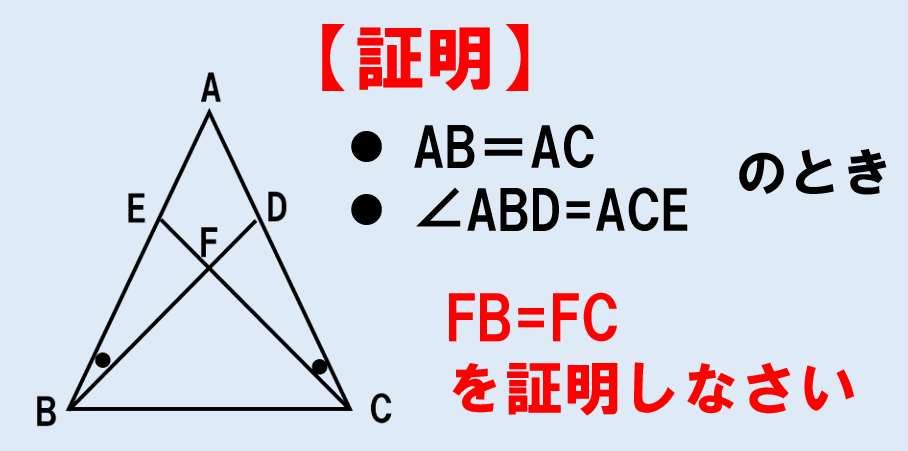



中2数学 2角が等しい三角形 二等辺三角形の長さを用いた証明 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強




三角形 Wikipedia




不等辺三角形 至急ご回答お待ちしております 不等辺三角形について その他 学校 勉強 教えて Goo
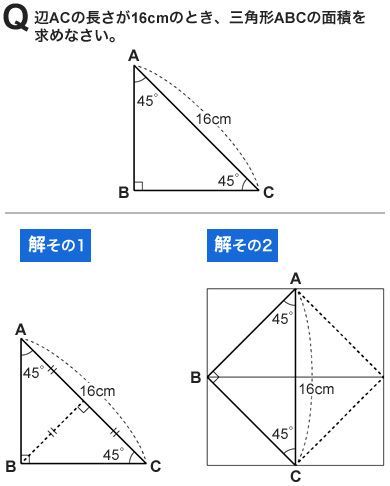



256が解ける子解けない子の差 4つの解法をすぐ思いつくか 2ページ目 President Online プレジデントオンライン
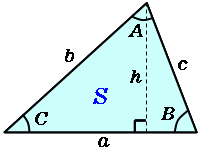



不等辺三角形 高精度計算サイト
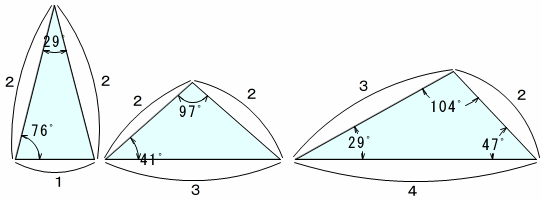



3 4 5の三角形で 本当に直角ができる Note Board




不等辺三角形 幻冬舎文庫 内田 康夫 本 通販 Amazon




数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project
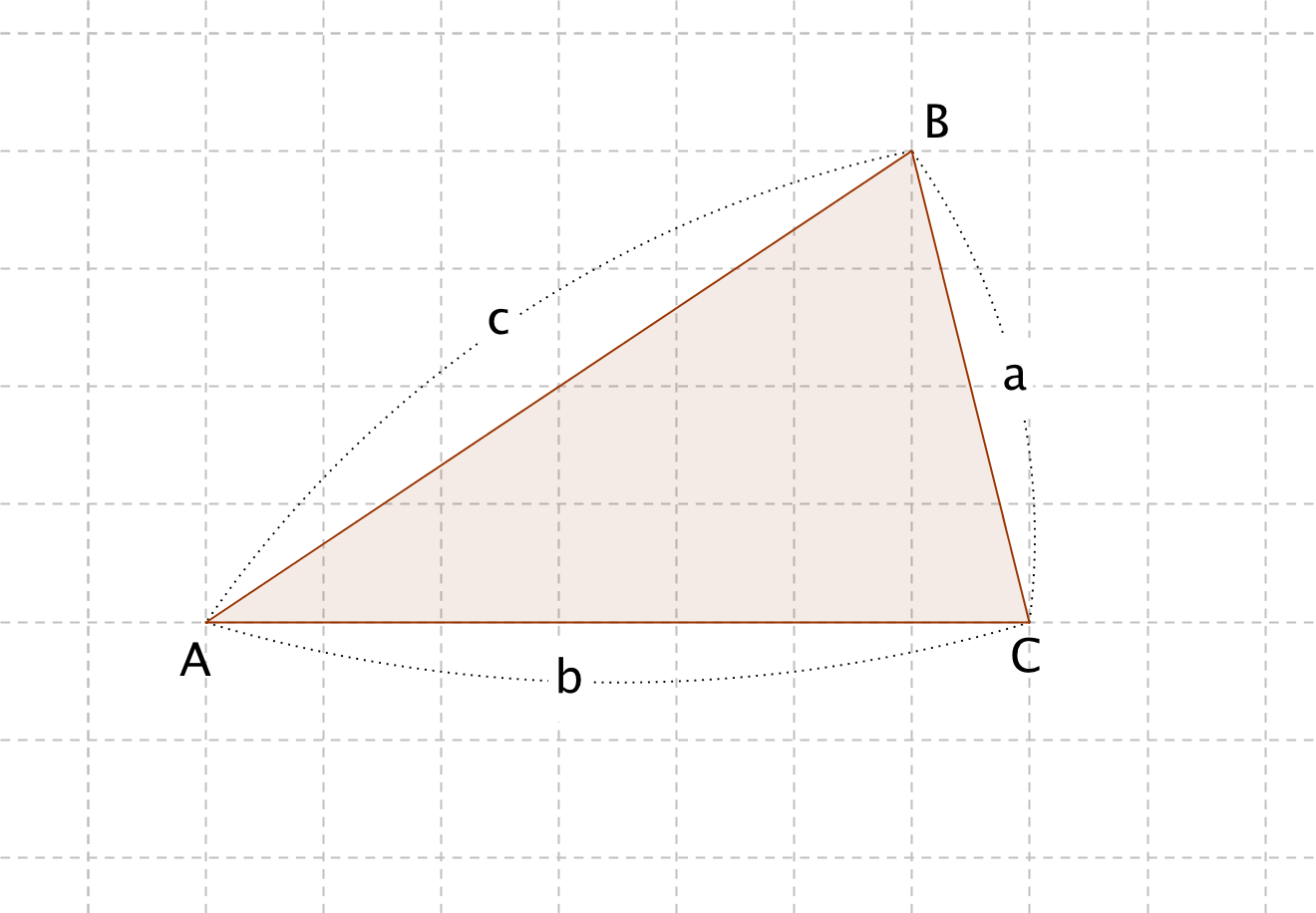



C言語入門 入力した3辺の長さから三角形の種類を判別 Webkaru




不等辺三角形の定理 短編 あがた愛 ボーイズラブマンガ Kindleストア Amazon




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強




直角三角形の辺を求める Youtube




不等辺三角形の欠けている辺の長さ 21
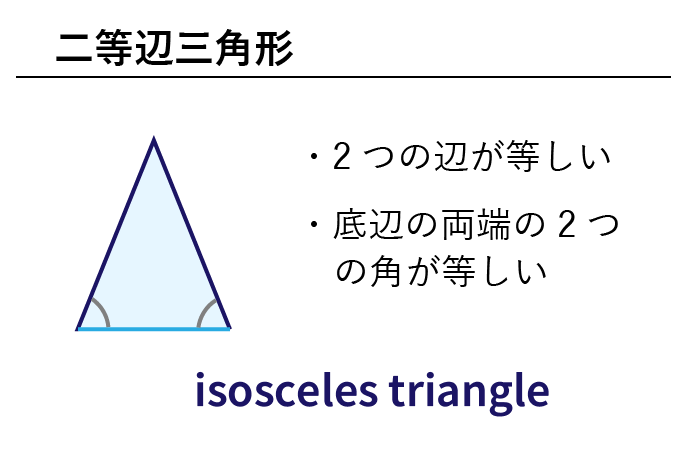



数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project
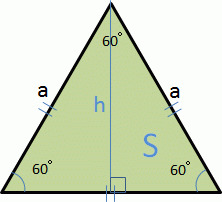



三角形の公式 Wakatta
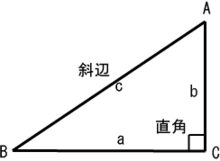



直角三角形 Wikipedia



Math 90 30 60 の直角三角形 辺の長さで成り立つこと 働きアリ
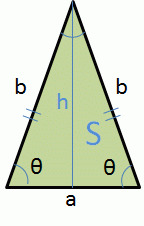



三角形の公式 Wakatta




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
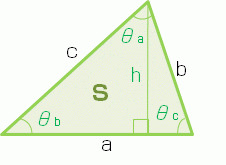



三角形の公式 Wakatta




種明かし Imujii S Page




マイヤーズの三角形問題 テストの基礎 Qbookアカデミー



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



三角形の計算 Google Play のアプリ




号 テスト設計 技法 の必要性 Kouichi Akiyama Note




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
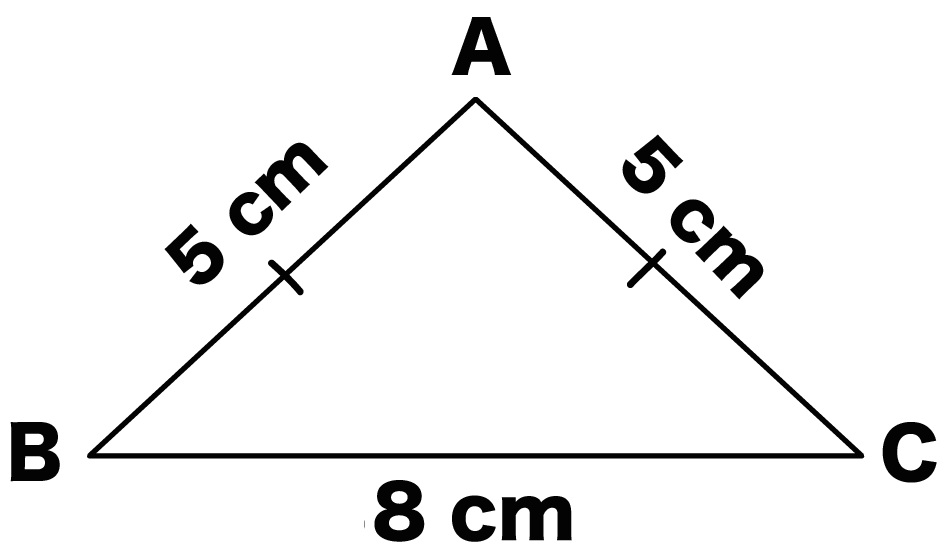



簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強



0 件のコメント:
コメントを投稿